[백준/BOJ] 2342 - Dance Dance Revolution (G3/Java)

문제 링크

2342번: Dance Dance Revolution

 

🏷️ 카테고리

# 다이나믹 프로그래밍

 

⏳ 시간복잡도

 

 

📒 해설

오락실에 있는 DDR 게임을 할 때 버튼을 어떤 발로 밟을 때, 가장 적은 힘이 드는지를 구하는 문제입니다. N이 작다면 완전 탐색을 통해 풀 수도 있지 않을까 싶지만, N이 10만이기 때문에, 이용할 수 없는 문제였습니다. 상태 공간 트리를 그린다면, 중복되는 구간이 많이 나오기 때문에, 그림을 그려본다면 빠르게 DP 문제라는 것을 알 수 있었습니다.

📜 문제 조건

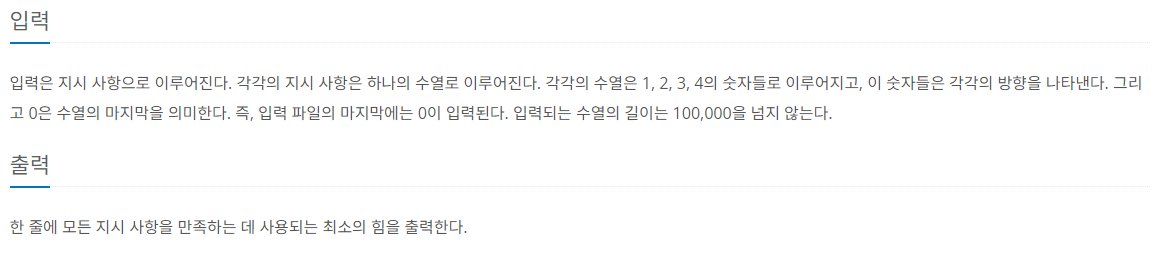
Dance Dance Revolution 문제에서 주어진 조건을 정리하면 다음과 같습니다.

• 주어진 발판은 0(가운데), 1(위), 2(왼쪽), 3(아래), 4(오른쪽)가 있다.
• 주어진 입력은 승환이가 밟아야 하는 버튼을 뜻하고, 0이 주어지면 종료한다.
• 이미 밟고있는 발판이 있다면, 무조건 그 발로 밟아야 한다.
• 발판을 밟을 때에는 힘이 드는데, 동일한 발판인 경우 1, 인접한 지점일 경우 3, 반대편 방향일 경우는 4의 힘이 들고, 0에서 갈 때엔 2가 든다.
• 모든 발판을 밟았을 때, 최소로 드는 힘을 출력해라.

🔍 문제 접근

완전 탐색으로 문제를 풀 수 없을 것 같아서, 어떤 경우가 있을지에 대해서 생각을 해보며 상태 공간 트리를 작성해봤습니다.

 

위의 트리를 보면, 마지막 depth에서는 동일한 쌍이 나오는 것을 볼 수 있습니다. 그럼 그 값을 저장하면 나중에 또 이용할 수 있을 것이라고 생각했습니다. 그렇다면 어떤 값을 저장할지에 대해서 생각해보아야 합니다.

 

 

어떤 값을 저장할까

 

해당 문제를 보았을 때, 기본적으론 재귀적 호출을 통해서 비용을 계산하려고 했습니다. 예를 들면 (1,0)에서 2 발판을 만났을 때의 비용을 1->2의 비용 vs 0->2 비용을 계산해서 더 작은 방향으로 선택하려고 했습니다. 하지만 그 다음 이동하는 비용들을 계산하려고 할 때, 경우가 고정되어 있다는 사실을 알았습니다. 위의 그림의 마지막 depth에서는 각 값들이 2번씩 나오는 것을 볼 수 있습니다. 동일한 발판을 밟고있는 상황에서 발생할 수 있는 케이스는 당연히 같을 것입니다. 위에서 든 예 처럼 (1,0)이 2 발판을 만났다면 (2,0) 혹은 (1,2) 의 케이스밖에 없다는 이야기입니다. 

 

그렇다면 depth의 발판을 밟고 있을 때의 비용을 저장한다면, 이후에 등장하는 케이스에서 재활용을 하면 반복 횟수를 줄일 수 있다고 생각했습니다.

 

정리하자면 특정 depth A는 하위 depth A+1에서 왼발로 A로 이동하기 위한 비용과, 마지막 depth N부터 A+1까지 이동하기 위한 최소 비용 VS 오른발로 A로 이동하기 위한 비용과, 마지막 depth N부터 A+1까지 이동하기 위한 최소 비용 중 작은비용을 기록하는 것입니다.

 

해당 방법을 통해 2가지 방법으로 문제를 풀어보았다.

 

🔑 문제 풀이 1 - 3차원 배열 이용

 

사용 변수

static int[][] cost = { // 각 위치에서 다른 위치로 이동하는 비용
        {1,2,2,2,2},
        {1,1,3,4,3},
        {1,3,1,3,4},
        {1,4,3,1,3},
        {1,3,4,3,1}
};
static int[][][]dp; // DP Table depth, left, right
static int[] command; // 명령어

주석에서도 작성했지만, DP테이블은 3차원으로 구성했고, 각각 현재 depth, 왼발의 위치, 오른발의 위치를 나타내고 저장되는 값은 해당 상황에서의 최소 비용을 기록한다.

 

메인 로직

/*
    현재 depth에 저장할 비용은 다음 발판을 (왼발로 밟는 경우의 비용 + 그 경우의 수까지의 최소 비용) vs (오른발로 밟는 경우의 비용 + 그 경우의 수까지의 최소 비용)
 */
private static int ddr(int depth, int left, int right){
    if(depth == command.length-1)
        return 0;

    if(dp[depth][left][right] != 0) return dp[depth][left][right];

    int next = command[depth];

    if (next == left || next == right) {
        dp[depth][left][right] = ddr(depth+1, left, right) + 1;
    } else{
        dp[depth][left][right] = Math.min(ddr(depth+1, Math.min(next,right), Math.max(next,right)) + cost[left][next],
                ddr(depth+1, Math.min(left,next), Math.max(left,next)) + cost[right][next]);
    }
    return dp[depth][left][right];
}

 

위에서 설명했듯이, 현재 뎁스의 현재 발 상태 (dp[depth][left][right])에는 왼발을 다음 방향으로 이동한 경우와 오른발을 다음 방향으로 이동한 경우의 비용 중 최소값을 저장한다.

이때, 이미 밟고있는 케이스에는 그대로 간다고 했으니 그 경우는 +1을 해주고 넘어간다.

 

ddr(depth+1, Math.min(next,right), Math.max(next,right))

위처럼 left,right에 값을 넣어줄 때, min, max를 이용하는 이유는  (0,1)과 (1,0)은 동일한 경우이기 때문이다.

전체 코드

import java.io.*;
import java.util.*;


public class Main {

    static BufferedReader br = new BufferedReader(new InputStreamReader(System.in));

    static int[][] cost = {
            {1,2,2,2,2},
            {1,1,3,4,3},
            {1,3,1,3,4},
            {1,4,3,1,3},
            {1,3,4,3,1}
    };
    static int[][][]dp;
    static int[] command;
    public static void main(String[] args) throws IOException {
        StringTokenizer st = new StringTokenizer(br.readLine());

        command = new int[st.countTokens()];
        for (int i = 0; i < command.length; i++) {
            command[i] = Integer.parseInt(st.nextToken());
        }

        dp = new int[command.length][5][5];

        System.out.println(ddr(0,0,0));


    }

    /*
        현재 depth에 저장할 비용은 다음 발판을 (왼발로 밟는 경우의 비용 + 그 경우의 수까지의 최소 비용) vs (오른발로 밟는 경우의 비용 + 그 경우의 수까지의 최소 비용)
     */
    private static int ddr(int depth, int left, int right){
        if(depth == command.length-1)
            return 0;

        if(dp[depth][left][right] != 0) return dp[depth][left][right];

        int next = command[depth];

        if (next == left || next == right) {
            dp[depth][left][right] = ddr(depth+1, left, right) + 1;
        } else{
            dp[depth][left][right] = Math.min(ddr(depth+1, Math.min(next,right), Math.max(next,right)) + cost[left][next],
                    ddr(depth+1, Math.min(left,next), Math.max(left,next)) + cost[right][next]);
        }
        return dp[depth][left][right];
    }
}

결과

 

🔑 문제 풀이 2 - 2차원 배열 이용

 

사용 변수

static int[][]dp; // 2차원 배열
static int[] command;

기존에 왼발, 오른발을 2차원 배열로 표현해 전체가 3차원 배열이 되었던 것을, 비트마스킹으로 표현하여 왼발, 오른발의 값을 1차원으로 줄여주었다.

 

입력

int count;
command = new int[100000];
for (count = 0; ; count++) {
    int input = sc.nextInt();
    if (input == 0) break;
    command[count] = 1 << input;
}
dp = new int[count+1][1<<5];

 

 

왼발과 오른발을 비트로 표현하기로 했기 때문에 다음 발판 역시 비트로 표현해주었다.

dp테이블에 발 위치를 표현할 때 1<<5로 한 이유는 발판의 경우가 총 5개이기때문이다.

 

비용 계산

private static int calcCost(int l, int r) {
    // 2배 차이 나면 3, 같으면 1, 4배 차이나면 4

    if(l == 0 || r == 0)
        return 2;
    if(l == r)
        return 1;
    else if(l << 2 == r || r << 2 == l)
        return 4;
    else
        return 3;

}

 

 

발판을 비트로 관리하기 때문에, 배열을 통해 비용관리가 어려워져 따로 메서드를 제작했다. 비트 상황에서 4배가 차이나면 서로 반대 상황인 것으로 4, 같다면 1, 그 외에는 3을 리턴한다.

 

메인 로직

private static int ddr(int depth, int left, int right){
    if(depth == dp.length-1)
        return 0;

    int cur = left + right;
    if(dp[depth][cur] != 0) return dp[depth][cur];

    int next = command[depth];

    if (next == left || next == right) {
        dp[depth][cur] = ddr(depth+1, left, right) + 1;
    } else{
        dp[depth][cur] = Math.min(ddr(depth+1, next,right) + calcCost(next,left),
                ddr(depth+1, next,left) + calcCost(next,right));
    }
    return dp[depth][cur];
}

 

전체 코드

 

static PScanner sc = new PScanner(System.in);

static int[][]dp;
static int[] command;

public static void main(String[] args) throws IOException {

    int count;
    command = new int[100000];
    for (count = 0; ; count++) {
        int input = sc.nextInt();
        if (input == 0) break;
        command[count] = 1 << input;
    }
    dp = new int[count+1][1<<5];

    System.out.println(ddr(0,0,0));
}

private static int ddr(int depth, int left, int right){
    if(depth == dp.length-1)
        return 0;

    int cur = left + right;
    if(dp[depth][cur] != 0) return dp[depth][cur];

    int next = command[depth];

    if (next == left || next == right) {
        dp[depth][cur] = ddr(depth+1, left, right) + 1;
    } else{
        dp[depth][cur] = Math.min(ddr(depth+1, next,right) + calcCost(next,left),
                ddr(depth+1, next,left) + calcCost(next,right));
    }
    return dp[depth][cur];
}

private static int calcCost(int l, int r) {
    // 2배 차이 나면 3, 같으면 1, 4배 차이나면 4

    if(l == 0 || r == 0)
        return 2;
    if(l == r)
        return 1;
    else if(l << 2 == r || r << 2 == l)
        return 4;
    else
        return 3;

}

 

결과